How Calculate Polygon Area in a Software
Learn how to calculate the area of any polygon in a software. Calculating the area of a polygon is essential for determining the size of an object, precise measurements, or classifying its category. This process often involves utilizing algorithms like semantic segmentation.
Understanding Polygon Area Calculation
To calculate the area of a polygon, it is important to understand the concept of polygon area calculation. The area of a polygon refers to the space enclosed by its boundaries. It is a fundamental measurement used in various fields such as mathematics, engineering, surveying, and architecture.
Polygon area calculation involves determining the total area covered by a polygon using its side lengths, angles, or other relevant parameters. This calculation can be done using different methods, depending on the type of polygon and the available information. By understanding the basics of polygon area calculation, you can easily calculate the area of any polygon.
Real-World Applications of Polygon Area Calculation
Polygon area calculation has numerous real-world applications across various fields. Some examples include:
- Architecture and construction: Architects and engineers use polygon area calculation to determine the size and area of rooms, buildings, and structures. This information is crucial for designing and planning construction projects.
- Land surveying: Surveyors use polygon area calculation to measure and calculate the area of land parcels. This data is used for property boundaries, land valuation, and land development purposes.
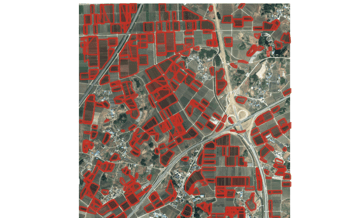
- Geographic information systems (GIS): GIS professionals utilize polygon area calculation to analyze and visualize spatial data. It helps in understanding the distribution and characteristics of different geographic features.
- Environmental science: Environmental scientists use polygon area calculation to calculate the area of habitats, study the impact of land use changes, and analyze biodiversity patterns.
- Surveillance and Reconnaissance: For example, if we use SAR or EO reconnaissance satellites to capture images of the enemy airfields, we may be able to detect an airplane, but we may have difficulty detecting what type of airplane it is. In this case, estimating the size of the plane can be useful in estimating whether the plane is a fighter, bomber, or UAV.
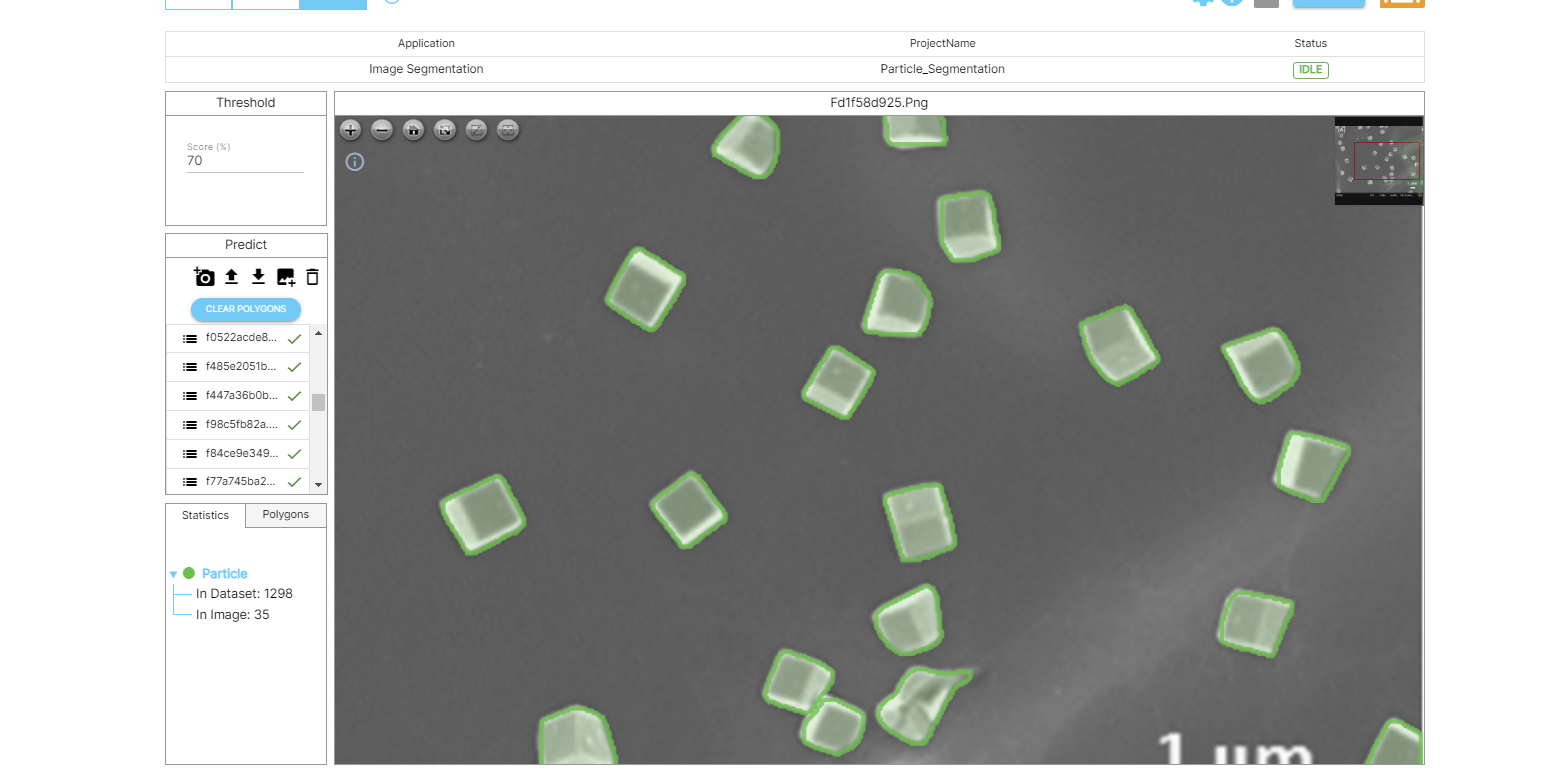
- Metrology and Inspection: The precise measurements of gates, metals, and defects captured in micrographs play a pivotal role in the inspection and analysis of semiconductor and nano materials. The area measurements not only help identify defects and measure the size of MOSFETs but also pave the way for automation in inspection tasks.
By integrating semantic segmentation and polygon area calculation, we can gain valuable insights for nanomaterial and semiconductor manufacturing.
A List of Polygon Area Calculation Algorithms
Computing the area of a polygon in a 2D Cartesian coordinate system involves various algorithms, each with its own advantages and use cases. Here are some commonly used algorithms:
-
Shoelace Formula (Gauss's Area Formula):
- This formula calculates the area of a simple polygon based on the coordinates of its vertices.
- As mentioned earlier, it sums up the products of consecutive vertex coordinates and calculates the absolute value of half the sum.
- This formula works well for both convex and concave polygons.
- Time complexity: O(n), where n is the number of vertices.
-
Triangle Decomposition:
- Decompose the polygon into triangles using a common vertex and calculate the area of each triangle.
- Sum up the areas of all triangles to get the total area of the polygon.
- This approach works for any polygon, including concave polygons and polygons with holes.
- Time complexity: O(n), where n is the number of vertices.
-
Cross Product:
- Divide the polygon into trapezoids by drawing a horizontal line at the lowest vertex (or the highest if the polygon is concave).
- Calculate the area of each trapezoid using the cross product of vectors formed by consecutive vertices.
- Sum up the areas of all trapezoids to get the total area of the polygon.
- Time complexity: O(n), where n is the number of vertices.
-
Pick's Theorem:
- This theorem states that the area of a polygon with integer coordinates whose vertices lie on lattice points (points with integer coordinates) can be calculated using a simple formula involving the number of lattice points inside the polygon and the number of lattice points on the boundary.
- While Pick's Theorem is elegant and simple, it's limited to polygons with integer coordinates.
- Time complexity: O(n), where n is the number of lattice points inside or on the boundary of the polygon.
-
Monte Carlo Integration:
- Use random sampling to estimate the area of the polygon.
- Generate random points within a bounding box that encloses the polygon and count how many fall within the polygon.
- Use the ratio of points inside the polygon to total points sampled to estimate the area.
- This method is probabilistic and may require a large number of samples for accurate results.
- Time complexity: Depends on the number of samples required for desired accuracy.